Sine definition, a cornerstone of trigonometry, unravels the mathematical intricacies of periodic phenomena, from sound waves to the swinging of pendulums. Embark on a journey to understand its geometric interpretation, properties, and myriad applications.
Delving deeper, we’ll explore the sine function’s periodicity, amplitude, range, and symmetry, revealing its unique characteristics. An interactive graph will bring its behavior to life, while a comprehensive table summarizes its key features.
Definition of Sine
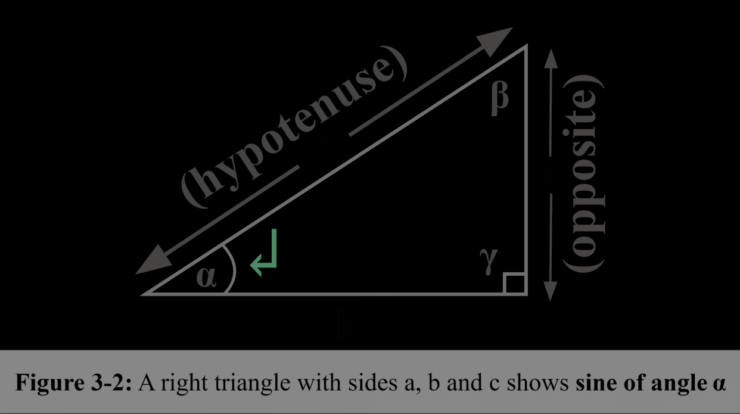
In mathematics, the sine of an angle is a function that measures the ratio of the length of the side opposite the angle to the length of the hypotenuse in a right-angled triangle.
Geometrically, the sine of an angle can be interpreted as the vertical coordinate of a point on the unit circle that lies on the terminal side of the angle.
In real-world applications, sine is used in a wide range of fields, including:
- Sound waves
- Pendulums
- Electrical circuits
Properties of Sine
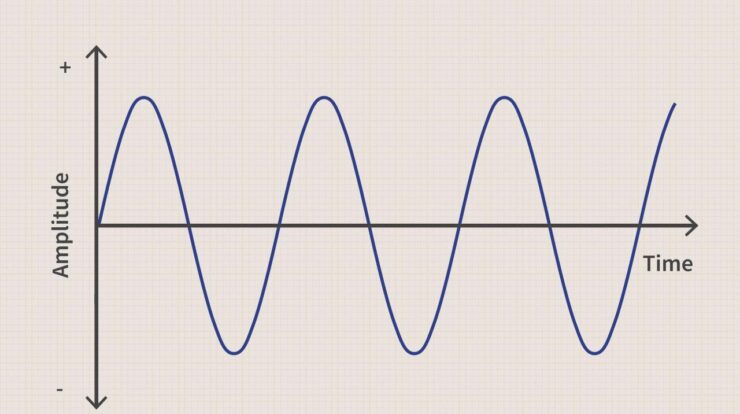
Sine is a periodic function with a period of 2π.
The amplitude of sine is 1, and its range is [-1, 1].
Sine is an odd function, meaning that sine(-x) = -sine(x).
Sine Function Graph
The graph of the sine function is a wave that oscillates between -1 and 1.
| x | sin(x) |
|---|---|
| 0 | 0 |
| π/2 | 1 |
| π | 0 |
| 3π/2 | -1 |
Applications of Sine: Sine Definition
Sine is used in a variety of applications, including:
- Sound waves:Sine waves are used to represent the sound waves that we hear.
- Pendulums:The period of a pendulum is proportional to the sine of the angle at which it is released.
- Electrical circuits:Sine waves are used to represent the voltage and current in AC circuits.
Related Trigonometric Functions
Sine is one of three trigonometric functions, the other two being cosine and tangent.
The sine, cosine, and tangent functions are related by the following identities:
- sin²x + cos²x = 1
- tanx = sinx / cosx
Last Point
In conclusion, sine definition provides a powerful tool for modeling and analyzing oscillatory motion. Its applications extend far beyond mathematics, enriching fields such as physics, engineering, and acoustics. Understanding sine empowers us to comprehend the rhythmic patterns that shape our world.
Detailed FAQs
What is the geometric interpretation of sine?
Sine is the ratio of the opposite side to the hypotenuse in a right triangle.
How is sine used in real-world applications?
Sine is used in modeling sound waves, analyzing pendulum motion, and designing electrical circuits.
What is the difference between sine, cosine, and tangent?
Sine, cosine, and tangent are all trigonometric functions that relate the angles and sides of a right triangle. Sine is the ratio of the opposite side to the hypotenuse, cosine is the ratio of the adjacent side to the hypotenuse, and tangent is the ratio of the opposite side to the adjacent side.